Area Related to Circles Class 10: A Complete Guide

Understanding the topic of area related to circle Class 10 can be simple and enjoyable with the right approach. In this guide, we will break down key concepts, formulas, and problem-solving techniques in an easy-to-understand way. By the end of this blog, you’ll feel confident tackling any question about area related to circle Class 10.
What Does “Area Related to Circle Class 10” Mean?
The topic “area related to circle class 10” focuses on calculating and understanding the different regions formed by a circle. These include:
- The area of the entire circle
- The area of sectors
- The area of segments
These concepts are part of geometry and are often used in real-life scenarios like designing, architecture, and even games. Let’s learn about these areas in detail.
Basic Terms You Need to Know
Before diving into formulas, let’s cover some important terms:
- Circle: A shape where all points are equidistant from the center.
- Radius (r): The distance from the center to any point on the circle.
- Diameter (d): Twice the radius (d = 2r).
- Circumference: The total distance around the circle (C = 2πr).
- Sector: A slice of the circle formed by two radii.
- Segment: A part of the circle separated by a chord.
Knowing these terms will help you understand the topic better and make solving problems easier.
Formulas for Areas Related to Circles
Here are the key formulas you’ll use for solving problems in area related to circle Class 10:
- Area of a Circle: πr²
- Example: If the radius is 7 cm, the area is 22/7 × 7 × 7 = 154 cm².
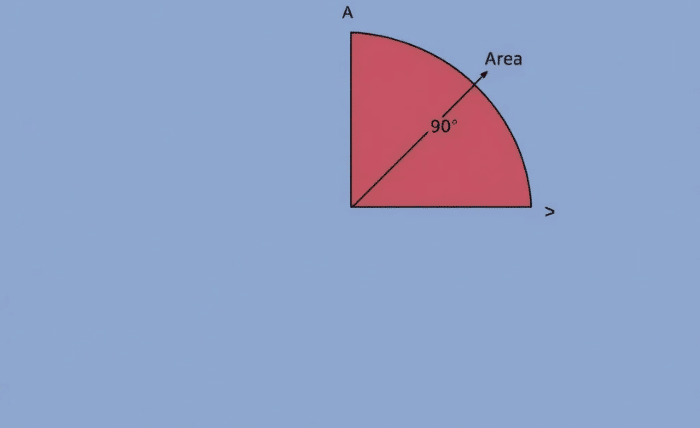
- Area of a Sector: (θ/360) × πr²
- Example: For a 90° sector and radius 7 cm, the area is (90/360) × 22/7 × 7 × 7 = 38.5 cm².
- Area of a Segment:
- Formula: Area of Sector – Area of Triangle
- Example: Calculate the segment’s area by finding both the sector and triangle areas.
- Circumference of a Circle: 2πr
- Length of an Arc: (θ/360) × 2πr
- Example: For a 120° arc of a circle with radius 10 cm, the length is (120/360) × 2 × 3.14 × 10 = 20.94 cm.
These formulas will help you solve most problems related to circles. It’s essential to practice them regularly to build your confidence.
Common Problems and Solutions
Let’s go through a few example problems related to the topic of “area related to circle class 10.”
Problem 1: Finding the Area of a Sector
A circle has a radius of 10 cm. Find the area of a 120° sector.
Solution:
- Use the formula for the area of a sector: (θ/360) × πr².
- Substitute the values: (120/360) × 3.14 × 10 × 10.
- Simplify: (1/3) × 3.14 × 100 = 104.67 cm².
Problem 2: Finding the Area of a Segment
A circle has a radius of 14 cm. A chord divides the circle into two segments, and the angle subtended by the chord at the center is 60°. Find the area of the smaller segment.
Solution:
- Calculate the area of the sector: (60/360) × 22/7 × 14 × 14 = 102.67 cm².
- Find the area of the triangle using trigonometry: ½ × r² × sin (60°).
- For radius 14 cm, this is 0.5 × 14 × 14 × (√3/2) = 84.87 cm².
- Subtract the triangle’s area from the sector’s area: 102.67 – 84.87 = 17.8 cm².
Problem 3: Calculating the Shaded Region
A square with a side of 14 cm is inscribed in a circle. Find the area of the circle outside the square.
Solution:
- Calculate the diagonal of the square: √2 × side = √2 × 14 = 19.8 cm.
- The diagonal is the diameter of the circle, so the radius is 19.8/2 = 9.9 cm.
- Find the area of the circle: πr² = 3.14 × 9.9 × 9.9 = 307.88 cm².
- Find the area of the square: side² = 14 × 14 = 196 cm².
- Subtract the square’s area from the circle’s area: 307.88 – 196 = 111.88 cm².
Applications of Areas Related to Circles
The concepts in “area related to circle class 10” are not limited to textbooks. They are used in:
- Architecture: Designing round windows and arches.
- Gardening: Planning circular flower beds and fountains.
- Engineering: Creating round gears and wheels.
- Sports: Designing tracks, circular arenas, and stadiums.
- Agriculture: Measuring circular plots for irrigation.
Understanding these applications can make the subject more relatable and practical.
How to Tackle Area-Related Questions Effectively
- Understand the Question: Carefully read and identify what is being asked.
- Draw a Diagram: Sketching helps visualize the problem clearly.
- Label the Diagram: Mark radii, angles, and other dimensions.
- Write Down the Formula: Use the relevant formula based on the question.
- Simplify the Values: Solve step by step to avoid errors.
- Check Units: Ensure the answer is in the correct units (e.g., cm²).





